PARADOKS NEDİR?

Paradoks, görünüşte doğru olan bir ifade veya ifadeler topluluğunun bir çelişki yaratması veya sezgiye karşı bir sonuç yaratmasıdır. Çoğunlukla, çelişkili gözüken sonuç veya sonuçların aslında çelişkili tarafları vardır. Paradoks teriminin karşılığı olarak Türkçe’de yanıltmaç ve çatışkı sözcükleri de kullanılmaktadır.

Ayrıca kendi içinde çelişen veya tam tersi şekilde sonuç olarak doğru olan fakat absürd veya çelişkili gözüken bir ifadeye (veya ifadelere/ifadeler bütününe) de paradoks denmektedir. Kökleşmiş inanışlara aykırı olarak ileri sürülen düşünce olarak da tanımlanabilir. Yani bir nevi çelişkidir.

MATEMATİK PARADOKSLARI NELERDİR?

 

DOĞRU PARÇASI PARADOKSU:

           Önce doğru parçasının tarifini yapalım:Doğru Parçası: Başlangıcı ve sonu olan ve sonsuz adet noktadan oluşan doğru. Pekiyi nokta nedir?
Nokta: Kalemin kağıda bıraktığı en küçük iz veya belirti. Malumdur ki noktanın boyutu yoktur. O halde dikkat. Paradoks başlıyor:

          Noktanın boyutu olmadığına göre iki noktanın yan yana gelmesi bir şey ifade etmez. 100 nokta veya 1 milyar nokta da yan yana geldiğinde herhangi bir şekil oluşturmaz.( Çünkü şekil oluşturması için gerekli olan boyut özelliğini sağlamıyor) Bu şuna benzer ki; sıfır ile sıfırın toplamı yine sıfırdır. Milyarlarca sıfırı toplasak 'yarım' dahi etmez. O halde doğrunun tanımında bir hata var. Çünkü sonsuz adet noktanın yan yana gelmesi bir şey ifade etmez! Noktanın çok az da olsa boyutu olduğunu kabul etmemiz gerekir. Bu sefer de noktanın tarifi hatalı olur.

          Noktayı boyutlu kabul edelim.  Karşımıza bir paradoks daha çıkar; doğru parçasında sonsuz adet nokta olduğuna göre doğru parçasının da uzunluğu sonsuz olmalıdır. Çünkü çok az da olsa boyutu olan bir şeyden sonsuz adedi yan yana gelirse sonsuz uzunluk olur.  

2+2=5  ?  PARADOKSU:

X = Y ................................................olsun
X² = X.Y............................................eşitliğin her iki tarafını 'X' ile çarptık.
X² - Y² = XY - Y²..............................her iki taraftan 'Y²' çıkardık.
(X + Y).(X - Y) = Y.( X-Y )...............sol tarafı çarpanlara ayırdık, sağ tarafı 'Y' parantezine aldık.
( X + Y ) = Y.....................................( X - Y )'ler sadeleşti.
X + X = X..........................................X = Y olduğundan,
2.X = X..............................................'X' leri topladık.
2 = 1 ................................................'X' ler sadeleşti.
3 + 2 = 1 + 3....................................her iki tarafa '3' ilâve ettik.
5 = 4..................................................buradan,
5 = 2 + 2.......................................'4'ü, '2+2'  şeklinde yazdık.  HATA NEREDE?

 

CANTOR PARADOKSU:

          George Cantor'a göre bir kümenin alt kümelerinin eleman sayısı, asıl kümeden daha fazladır. Ancak bu kaide, "Bütün kümelerin kümesi" için de geçerli midir?

"Bütün kümelerin kümesi", X olsun. Öyle ise her alt kümesi kendisinin elemanıdır. X'in "Alt kümeleri kümesi" de X'in alt kümesidir. Yani:

2ª Ì X   (2 üzeri a, alt küme X)  dir. Buradan şunu yazabiliriz:

card(2ª)  card(a)................1

Çünkü alt kümelerin kardinali asıl kümelerden küçüktür veya eşittir. Ancak Cantor Teoremine göre:

card(2ª) > card(a)...................2

olmalıdır. 1 ve 2 çelişmektedir. 

KARIŞIM PARADOKSU:

          Bir fincan sütümüz ve bir fincan da kahvemiz var. Bir kaşık sütten alıyoruz ve kahve fincanına döküyoruz. İyice karıştırıp oradan da bir kaşık alıyoruz ve süte döküyoruz. Şimdi sorumuz geliyor:

         Kahvedeki süt mü yoksa sütteki kahve mi daha fazladır?

          Cevap şaşırtıcı gelebilir ama karışım oranları eşittir. İşte ispatı:

          Kabul edelim ki karışımımız homojen olmasın. Meselâ kahveye kattığımız süt, tamamen dibe çöksün. Kahveden aldığımız miktar tabi ki sütten aldığımıza eşit olacaktır. Veya:

          İlk karışımdan sonra kaşığımızın yarısı süt, yarısı da kahve olsun. Bu sefer yine sütte yarım kaşık kahve, kahvede yarım kaşık süt bulunacaktır. Veya:

          İlk karışım homojen olsun. Aldığımız bir kaşık karışımın % 90 ını kahve, % 10 unu süt kabul edelim. Sütün % 90 ı kahvede kalmıştır. Sonuçta eksilen sütün yerini kahve dolduracağından karışım oranları eşit olur.  

BÜTÜN SAYILAR EŞİTTİR PARADOKSU:

           a ve b birbirinden farklı herhangi iki tamsayı ve c de bunların farkı olsun:

a-b=c
(a-b)(a-b)=c.(a-b)..............................her iki tarafı (a-b) ile çarptık.
a²-2ab+b²=ac-bc...............................parantezleri açtık.
a²-2ab+b²-ac=-bc.............................ac yi sol tarafa attık.
a²-2ab-ac=-bc-b²...............................b² yi sağ tarafa attık.
a²-ab-ac=ab-bc-b².............................2ab nin birini sağ tarafa geçirdik.
a(a-b-c)=b(a-b-c)..............................a ve b parantezine aldık.
a=b....................................................(a-b-c) ler sadeleşti.  (2+2=5 Paradoksunun benzeri) 

KARIŞIK BİR HESAP PARADOKSU:

              İki çocuk ayrı ayrı kalem satmaktadırlar. Her ikisinin de 30'ar tane kalemi vardır. Biri, 3 kalemi 10 TL'ye; diğeri de 2 kalemi 10 TL'ye vermektedir. İlki 30 kalemden 100 TL, diğeri de 150 TL kazanır. ( Toplam 250 TL.) Ertesi gün yine 30'ar kalemle evlerinden çıkarlar. Yolda karşılaştıklarında biri diğerine der ki:

-"Gel seninle ortak olalım. 60 (30+30) kalemin 5 (2+3) tanesini 20 (10+10)TL'ye satalım. Kazandığımız parayı da paylaşırız. Basit bir hesapla 60 kalemden 240 TL kazanırlar. Yani:

5 Kalem...............20 TL ise
60 Kalem..............x TL'dir.    Buradan;

x=(60.20)/5= 240 TL

Çocuklar, ayrı ayrı satış yaptıklarında toplam 250 TL kazanıyorlardı. Beraber sattıklarında neden 10 TL zarar ettiler?

 

1 kg = 1 ton ? PARADOKSU:

1 kg = 1000 gr.............(1)
2 kg = 2000 gr.............(2)

(1) ve (2) çarpılırsa:

2 kg = 2.000.000 gr
2 kg = 2.000 kg.............(2.000.000 gr = 2.000 kg)
2 kg = 2 ton..................(2.000 kg = 2 ton).  Dolayısı ile,
1 kg = 1 ton

 

HEMPEL PARADOKSU:

          Carl Hempel'e göre "Bütün kuzgunlar siyahtır!"

          Bu önermeyi iki şekilde ispatlayabiliriz:

a) Çok sayıda kuzgun görüp, hepsinin de siyah olduğunu tesbit ederek,
b) Siyah olmayan şeylerin, aynı zamanda kuzgun da olmadığını görerek.

          Bilinen şu ki çok sayıda siyah kuzgun ve yine çok sayıda siyah olmayan, aynı zamanda kuzgun da olmayan cisim vardır. Siyah olmayan tüm cisimler incelenmeden bu fikre varamayız. Kırmızı cisimler için bu uygulama yapılmamışsa "bazı kuzgunlar kırmızı " da olabilir. Bu sebeplerden Hempel paradoksu, "Tümevarım" ın itibarını sarsmıştır.

 

ARNAULD PARADOKSU:

Herkes bilir ki;

·         (Büyük Sayı / Küçük Sayı) ¹ (Küçük Sayı / Büyük Sayı) dır.
(5 / 2) ¹ (2 / 5) gibi

Ancak negatif sayılar bu kuralı bozar:
(3 / -3) = (-3 / 3)

Ayrıca;

·         (Büyük Sayı / Küçük Sayı) > 1 dir.
(4 / 3) > 1 gibi

Yine negatif sayılar için kural ihlâl edilir:
(3 / -1) < 1

Bu durum, matematikçi Arnauld'a mantıksız geldiği için negatif sayıların olmadığına hükmetti.

 

GALİLEO PARADOKSU:

Sonsuzlukla ilgili bir paradoks:

 

 

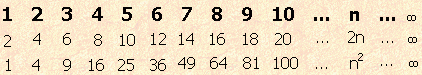
         Yukarıda ilk sırada pozitif tamsayılar, altında iki katları, en altta da kareleri var. İlk seri sonsuz olduğuna göre diğer seriler de sonsuz elemanlı. Ayrıca ilave olarak sayıların küplerini, üç katlarını, on katlarını, yarılarını, üçte birlerini de yazabiliriz. Hiçbir sonsuz da birbirine eşit değil.

 

EUPLİDES (KUM YIĞINI) PARADOKSU:

          Euplides, hiçbir zaman bir "kum yığını" oluşturulamayacağını iddia etmiştir. Çünkü bir kum tanesi, "yığın" değildir. Yanına bir tane daha koyarsak yine yığın oluşmaz. "Kum yığını" olmayan bir şeyin yanına (veya üzerine) kum tanesi koymakla yığın elde edemeyeceğimize göre Hiçbir zaman "kum yığını" oluşturamayız.

          Daha açık bir deyişle: Kabul edelim ki birer birer kum tanelerini biraraya getirelim. Hangi merhaleden sonra kumlar "yığın" oluşturur? Diyelim ki 'bir milyon' adet kum tanesi, bir yığın oluştursun. Dokuzyüz doksan dokuzbin dokuzyüz doksan dokuzu "kum yığını" kabul edilmeyecek mi? Edersek "1" eksiği de yığın olmaz mı? Yani hangi aşama bizim için "yığın" anlamına gelir?

 

-1=1 ? PARADOKSU:

 

 

 

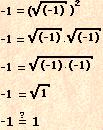
BERBER PARADOKSU: 

          Klasik paradokslardan biri daha:

         Bir berber, bulunduğu köydeki erkeklerden, yalnızca kendi kendini traş edemeyen erkekleri traş ediyor. Berberi kim traş edecek?
          Kendi kendine traş olsa;  kendisini traş edebildiği için  tanıma ters düşecek. Başkası traş etse; o kişi kendi kendine de traş olabiliyor demektir. (bkz Russel Paradoksu)

 

RUSSEL PARADOKSU:

1970 yılında 98 yaşında ölen Bertrand RUSSEL'ın çok bilinen paradoksu:

"Bir odada papa ve ben varım. Odada kaç kişiyiz?"   Cevap:
"Bir kişiyiz. Çünkü ben, aynı zamanda papayım"

Russel'ın "Kümeler" Paradoksu:

Russel'a göre iki çeşit küme var:

a) Kendisinin elemanı olan(ihtiva eden) kümeler.
b) Kendisinin elemanı olmayan kümeler.

Şimdi, "Kendisinin elemanı olmayan kümeler"in kümesine 'X' diyelim. X, kendisinin elemanı mıdır?

 

ZENO PARADOKSLARI

Zeno, matematik tarihindeki ilk büyük şüphecidir.  Paradoksları matematikçileri yıllarca uğraştırmış ve paradokslarının yol açtığı araştırmalar sonucu matematiğin gelişimine büyük katkı yapmıştır.
  Zeno’nun doğum ve ölüm tarihleri tam olarak bilinmemektedir.  Ancak tahminlere göre Zeno, M.Ö. 495 yılında İtalya’daki bir Yunan kolonisinde doğmuştur.  Doğduğu koloninin ismi Elea olduğundan Elea’lı Zeno olarak bilinir.
  Parmenides adında bir filozofun öğrencisi olan Zeno, hocasına M.Ö 449 yılında Atina’ya yapılan bir yolculukta eşlik etmiştir.  Bu yolculuğun, Zeno’nun geleceği açısından çok önemli olduğu düşünülmektedir.  Elea’ya geri döndüğünde politikaya girmiştir.  Bu dönemde şehrin gaddar yöneticisi olan Nearchus’a düzenlenen bir süikastta yer aldığı iddiasıyla tutuklanmıştır.  Bu suikasttaki rolü yüzünden öldürülene kadar işkenceye maruz kaldığı ve bu şekilde öldüğü söylenir.
  Zeno bir filozof ve mantıkçıydı.  Matematikçi değildi.  Bilinen tek yapıtı Epicheiremata’dır.  Bu eserinde özellikle, hocasının fikirleri ve kendi fikirleri üzerine yazılar bulunmaktadır.
  Zeno’nun asıl ünü paradokslarından gelmektedir.  Zeno’nun 40’a yakın paradoksu olduğu biliniyor fakat günümüze bunlardan yalnızca 8 tanesi kaldı.  Zaten Zeno’nun tek kitabının da tamamı şu anda bulunmamakta.  Kitabının bir bölümü günümüze kadar korunabilmiş.
  Zeno aslında hocası Parmenides’le aynı görüşlere sahip değildi.  Parmenides’in savunduğu felsefe, gerçeğin sadece bir tane ve değişmez olduğunu söylüyordu.  Ona gore, hareket, değişim, zaman ve çokluk kavramları küçük birer hayaldiler.  Zeno’nun paradoksları ise bu görüşün tam tersini kabul ederek yazılmışlardı.  Zeno’ya gore gerçeklik tek değildi, birçok gerçek olabilirdi, gerçek saçmaydı ve tezatlarla doluydu.

 

DİCHOTOMY PARADOKSU:

Hareket yoktur.  Çünkü bir hareketin olabilmesi için belirli bir zaman diliminde belirli bir mesafenin yapılmış olması gerekir.  Bunun için de istenilen mesafenin önce yarısı, sonar kalan mesafenin yarısı, daha sonra kalanın yarısı vb…gidilmesi gerekir.  Ancak her zaman gidilmemiş bir “kalan yolun yarısı” olacaktır.  Dolayısıyla hareket hiç başlamamıştır.

 

TAVŞAN - KAPLUMBAĞA PARADOKSU:

Hareketli bir tavşan hiçbir zaman kendisinden ilerdeki hareketli bir kaplumbağayı yakalayamaz.  Çünkü kaplumbağayı yakalaması için öncelikle, seçilen bir anda kaplumbağanın bulunduğu noktaya gelmesi gerekir.  Tavşan o noktaya gelene kadar kaplumbağa biraz daha ilerlemiş olur.  Daha sonra ilerideki kaplumbağanın o anda bulunduğu noktaya gidene kadar kaplumbağa biraz daha ilerler.  Sonuçta kaplumbağa hareketli olduğundan, tavşan, kaplumbağayı asla yakalayamaz.

 

OK PARADOKSU:

Zaman “an” lardan oluşmuştur.  “An”zamanın en küçük parçasıdır ve bölünemez.  Bir ok hareketli veya hareketsiz olsun, aslında ok hiçbir zaman hareket edemez.  Çünkü hareketin gerçekleşmesi için okun bir anın başlangıcında bir noktada, anın sonunda da başka bir noktada olması gerekir.  Ancak bunun olması için “an” ın bölünebilir olması gerekir ki bu da tanıma göre mümkün değildir. Dolayısıyla ok aslında hareket etmemiştir.

Not: Bu bölüm internetten alıntı yapılarak oluşturulmuştur.